The normal distribution in small numbers
|
A t-distribution (TD) is one of the derived (not fundamental), though very useful, statistical distributions. It is used while estimating a population mean from small sample sizes, where population standard deviation is not known. |
Most natural world stochastic phenomena can be characterized with the normal distribution. A normal distribution can be completely described with only two parameters: the mean and the standard deviation.
The central limit theorem states that the probability distribution function for mean values of a number of samples is approximately a normal distribution regardless of the actual population distribution, if sample size is large. Then, the population mean can be estimated from the z-score and normal distribution table as follows:
In the real world statistical estimations, sometimes the sample size is small and population standard deviation is not used (hence central limit theorem cannot be used). Then, the sample statistics from the sampling distribution does not conform to the normal distribution but to the TD.
The TD is based on the t-score:
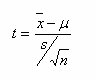
Where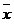 
is the sample mean,
μ is the population mean, s is the sample standard deviation and n is the sample size. The
distribution of the t statistic is called the TD.
A TD is similar to the standard normal distribution, because the mean of both is zero. However for small sample size (n<30), the standard deviation of TD is much larger than that of standard normal distribution (1). The extent that a TD differs from a normal distribution is measured by degrees of freedom, which is (sample size - 1). As the degree of freedom grows (sample size becomes large) and TD becomes similar to the normal distribution. Also, as the sample size increases, the difference between the z-score of the normal distribution and the t-score of the TD decreases.
Consider a scenario where the sample mean is 200, the standard deviation is 40, the sample size is 15 and the population mean is 220. We want to find the probability that for a sample size of 15, the sample mean will not be greater than 200.
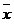≥ 200) = 3.7%Which means that for a population mean of 220 and sample mean 200 (with sample standard deviation 40), there is 3.7% probability that the sample mean will not exceed 200. Note that if a large sample value is used (for example n = 50), we should use z-score and not t-score to calculate this probability.
While normal and binomial distributions are the fundamental distributions of statistics which can describe many real world phenomena, some other distributions have also been derived in statistical mathematics and have their own special applications. They include beta distribution, gamma distribution, geometric distribution and logistic distribution.
For large sample sizes, a normal distribution can correctly describe the sampling distribution of any population. However, when the sample size is small and population standard deviation is not known, a t Distribution is useful. | |
|
The t-Distribution is similar to a standard normal distribution for large sample sizes, as the sample size decreases, a t Distribution starts to have a much different standard deviation from the standard normal distribution. Similarity of the t distribution and the standard normal distribution is expressed by the value of the degree(s) of freedom which is (sample size - 1). | |
The links below are specific questions and answers about statistics and how to use them.