What Is Correlation in Statistics

What is correlation in statistics: Correlation is a statistical concept that entails comparing two sets of data. The data can take various forms, such as distributions, lines, or curves. The crux of correlation revolves around the comparison itself. Through comparison, we can determine the degree of similarity or dissimilarity between the two sets of data.
Comparing two sets of data allows us to identify the nature of the relationship between them, which can either be positive or negative. In the case of positive correlation, an increase in values of one set of data is accompanied by a corresponding increase in the values of the other set. Conversely, a negative correlation indicates that as the values of one set of data increases, the other set’s data tends to decrease.
Correlation’s aptitude for uncovering the most intricate of relationships enables it to unmask the faintest of connections that may not necessarily be robust. A prime illustration of this is the weak positive correlation. This would indicate that the two datasets are mildly related. By comparing and contrasting two sets of data, correlation can help us glean valuable insights that can aid us in making informed decisions and precise predictions. Its capacity to unearth hidden links between different variables can catalyze breakthroughs in our understanding of complex phenomena.
The Measure of Comparison
The sample correlation coefficient, r has a range of -1 to 1. In general, the meaning is:
- 1 Perfect correlation. They are
identical. All data points are on the
line.
- 0 No correlation. The datasets are not related or correlated.
- -1 Perfect negative correlation. They are
statistical opposites. All data
points are on the line.
Of course, there are all decimal points between these numbers (the gray). You are basically looking for an r greater than .7 to say that you have a high correlation between the 2 entities. A strong negative correlation would be less than -.7.
The Equation
The sample correlation coefficient is obtained using this equation:
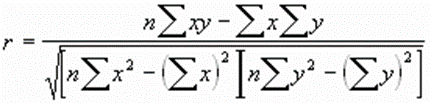
The Regression Calculation
The Regression Correlation Coefficient is a powerful tool that allows us to assess the degree of compatibility between the regression line and the underlying data from which it was derived. To better understand its significance, one can refer to the Simple Regression Calculation, where correlation assumes a pivotal role in gauging the efficacy of the regression line in fitting the data. By comparing the regression line's deviation from the actual values of the dependent variable, the correlation coefficient enables us to ascertain the line's capacity to predict the dependent variable's value with precision. In this manner, the regression correlation coefficient serves as a vital metric that can enhance our ability to make accurate predictions and informed decisions based on the data.
Frequently Asked Questions
What is correlation in statistics and how is it
defined?
Correlation is a statistical concept that entails the meticulous comparison of two sets of data, regardless of whether they are distributions, lines, or curves. The crux of correlation revolves around the comparison itself, allowing us to discern the degree of similarity or dissimilarity between the two sets of data. Once compared, we can identify the nuanced nature of the relationship between them, which can either be positive or negative.
How is correlation used to understand the relationships
between different variables?
The utility of correlation as a powerful mechanism for unraveling the complex interplay between variables cannot be overstated. Correlation can offer us a unique window into the inner workings of these variables. It can furnish us with a wealth of valuable insights that can aid us in making informed decisions and precise predictions. It facilitates the identification of links that may exist between different variables. It can serve as a catalyst for enhancing our comprehension of intricate phenomena. Consequently, correlation represents an indispensable tool for anyone seeking to unlock the secrets of our world.
What are the different types of correlation, and how do
we identify them?
The different types of correlation include positive correlation, negative correlation, and no correlation. Positive correlation indicates that as one set of data increases, the other set also tends to increase. Negative correlation, on the other hand, indicates that as one set of data increases, the other set tends to decrease. No correlation means that the datasets are not related or correlated at all.
How is correlation coefficient calculated, and what does it indicate about the strength of the correlation between two datasets?
The correlation coefficient, a statistical tool employed to quantify the degree of connection between two datasets, can be arrived at by dividing the covariance of the two datasets by the product of their standard deviations. This metric, which has a numerical range from -1 to 1, symbolizes the extent to which two datasets are positively or negatively related, with a coefficient of 1 indicating a perfect positive correlation, a coefficient of 0 representing no correlation, and a coefficient of -1 signifying a perfect negative correlation. Furthermore, the coefficient's size denotes the strength of the correlation between the two datasets, with a larger coefficient indicating a more robust relationship. For example, if the correlation coefficient exceeds 0.7, it is indicative of a high correlation between the two datasets, implying that the two phenomena under study are closely linked in a substantive manner.
