
Use regression to predict what comes next
There are two concepts of regression analysis that will help define what regression analysis is. If you understand these two concepts you will be well on your way to understanding what regression analysis is all about. You have probably already visited the Simple Regression Calculation page on this website that provides a "live" example of calculating linear regression. The results of this analysis are the two parameters that we want to discuss here.
On other pages of this website the value and importance of regression was discussed.
The emphasis here is on the interpretation and the validity of the analysis after it
has been preformed. There are many forms of regression including multiple regression,
exponential regression, logarithmic and even sine wave regression. The only
regression that will be discussed here is linear regression. It is the simplest,
but all the same principles apply to the other forms. The two concepts of
regression analysis that will be discussed are:
The first important concept that you must have when you view the results of a linear regression calculation is, you are given the parameters for the equation of a line.
The equation is obtained from two parameters:
On the Simple Regression Calculation
page you will see these two parameters in the results. The equation there is:
M is the slope and b is the y intercept. Looking at the graph you can see what the calculated line looks like.
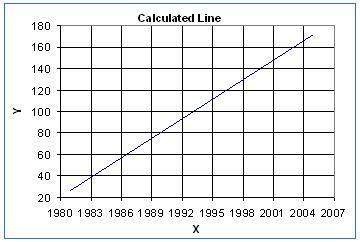
The second important concept that you must have when you view the results of a linear regression calculation is the correlation. The correlation is the r value. It can have a value between -1 and 1. How can do you know if you can rely on equation described above? The correlation helps you determine what level of confidence you can have. The closer to 1 that r is, the greater confidence you have. For a more detailed look at correlation go to Correlation Defined.
The two concepts of regression analysis that are most important are:
With these two concepts you can understand what the result of the calculation is and whether it can be relied on as a predicter.

The links below are specific questions and answers about statistics and how to use them.