Sign Test
The Sign test belongs to the confirmatory types of statistical tests. Most statistical tests require data to follow the
normal distribution. Many times, it is possible to transform data so that it follows the normal distribution; however
sometimes it is not possible, or sometimes the statistical sample size is so small that it becomes difficult to identify
if the data is normally distributed or not. In such scenarios, it becomes necessary to use a form of statistical testing,
where it is not necessary for the data to be normally distributed.
Statistical tests that do not require the normal distribution of the sample data are known as non-parametric tests.
Non-parametric tests are used when the data is not normally distributed. These tests are used to measure the significance of differences between two groups or treatment and control groups.
Sign test, Wilcoxon rank-sum test, and Mann-Whitney U test are some of these non-parametric tests.
Wilcoxon rank sum test is a non-parametric test of statistical hypothesis. It is used to compare the distributions of two samples and determine if they are from the same population.
The Wilcoxon rank sum test is a non-parametric test of statistical hypothesis. It is used to compare the distributions of two samples and determine if they are from the same population. It can be used for both independent samples and paired samples, but it cannot be used for dependent (related) samples.
The Wilcoxon rank sum test is based on the ranks of observations in each sample rather than their raw values, which makes it less sensitive to outliers than other parametric tests such as t-tests or ANOVA.
The Mann-Whitney U test is a non-parametric test for ranking data. It tests the null hypothesis that the two groups being compared are equally spread across the measurements of their variables.
Here you will find an example of the sign test.
The Sign Test is a non-parametric statistical test whereby very few assumptions are taken about the nature of the distribution being tested. This statistics hypothesis test works on the theory that there are equal probabilities of two outcomes. Instead of magnitude, this non-parametric test works on the direction of + and - sign of the observation. Since, there are just two choices i.e. + or -, so the NULL proportion is taken as p=0.5.
The sign test can be used when you have no idea about the distribution of values in your data set. The sign test is also useful if you need to make decisions quickly, as it is an easy and quick way to compare two populations without knowing their distributions.
The sign test is best used in exploratory data analysis.
When to use the Sign Test?
This test is used for the testing of the null hypothesis as well as in the situation where you want to find out if two groups are sized equally or not. It is also used in the case of sample t-test analysis as well as paired t test statistics.
Types of Sign Tests:
There are two types:
- One Sample Sign Test: In this test, the hypothesis is setup in a way that + and - signs are the values of the random variables that have equal size.
- Paired Sample Sign Test: It is also known as an alternative to the paired sample statistical t test. In this case, the + and - signs are used in the paired sample test or in the before/after study. The NULL hypothesis is setup in a way that either of the + and - signs are of equal size or the Population Mean values are equal to the Sample Mean value.
Sign Test Example
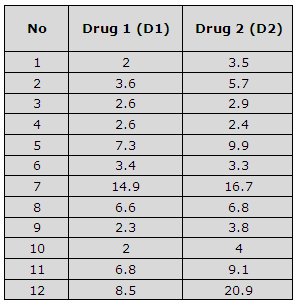
1. First of all, we get the random sample of data pairs (d1, d2). Below data pertains to the efficacy of two drugs. Suppose, we want to look out for the chances if any of the drugs works better than the other drug or not.
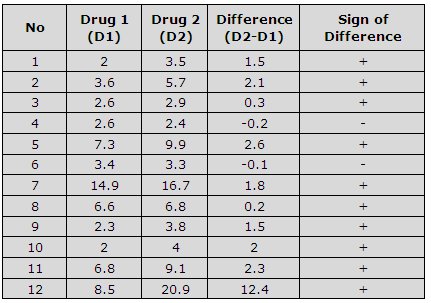


6. For H0 (p=0.5), assume that the Population Proportion of the + signs p = 0.5. The z-value corresponding to the Sample Proportion of the + signs x will be

7. Find the P-value by using the standard normal distribution table.
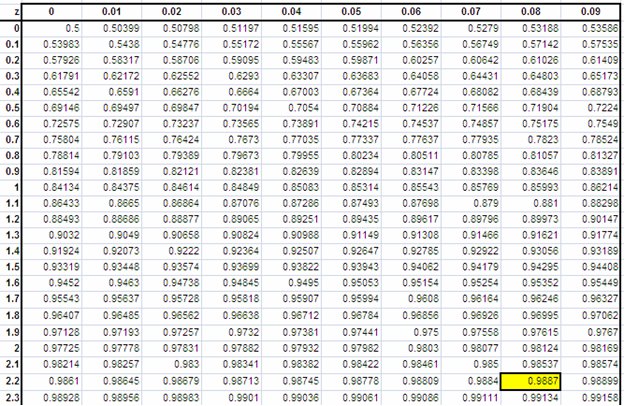

Summary
The Sign Test can be applied to both, the single observations or the pairs of related observations. However, the most useful application of this non-parametric test is in the before-and-after scenarios where the effects of a certain phenomenon on the same population are evaluated before and after the phenomenon is administered.
Q: Can you please provide a sign test example?
A: Sure! An example of the sign test is as follows:
Let's imagine that a brand-new medication is being evaluated to see if it can alleviate the symptoms of a particular health condition. A sample of twenty patients is chosen, with half receiving the new medication and half receiving a placebo. Each patient's reduced number of symptoms is recorded.
Seven out of ten patients who received the new medication experienced a reduction in symptoms, whereas only four of ten patients who received the placebo did so. We are able to carry out a sign test in order to ascertain whether the new medication is successful in reducing symptoms.
A sign test only takes into account the change's direction—whether there is an improvement or not—and not its magnitude. Following that, we count the number of "positive" signs, which in this instance would be the number of patients whose symptoms subsided as a result of taking the new medication.
In this instance, a positive change (reduction in symptoms) was experienced by 7 out of the 10 patients who received the new medication, while a positive change was experienced by 4 out of the 10 patients who received the placebo. The number of positive signs for each group would then be compared using the sign test to see if the difference is statistically significant.
